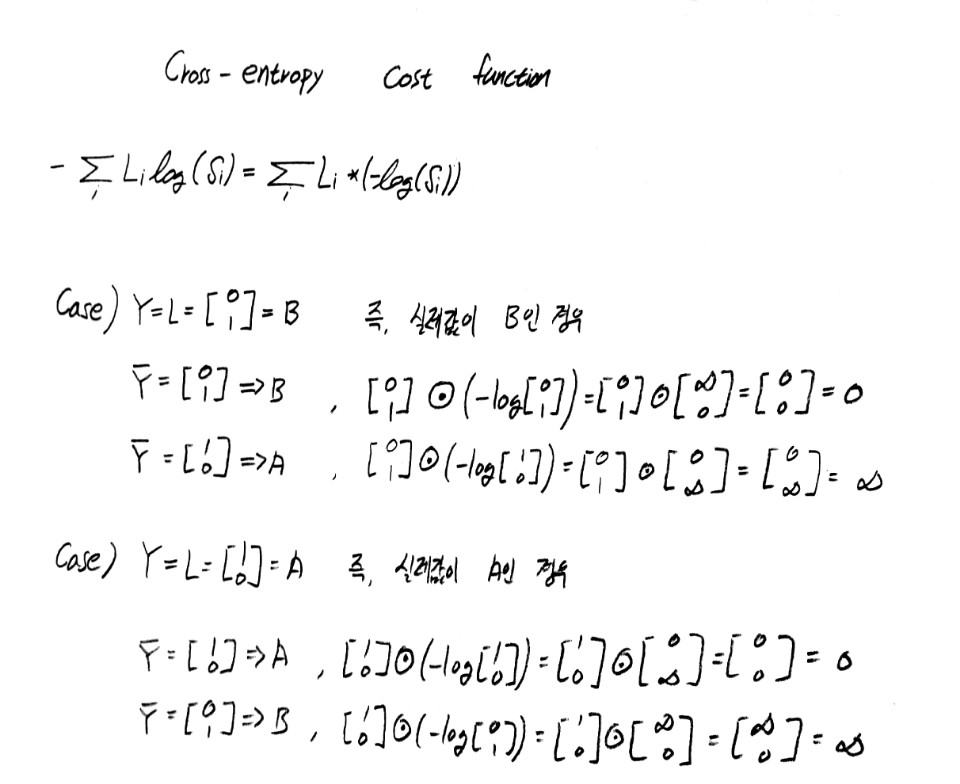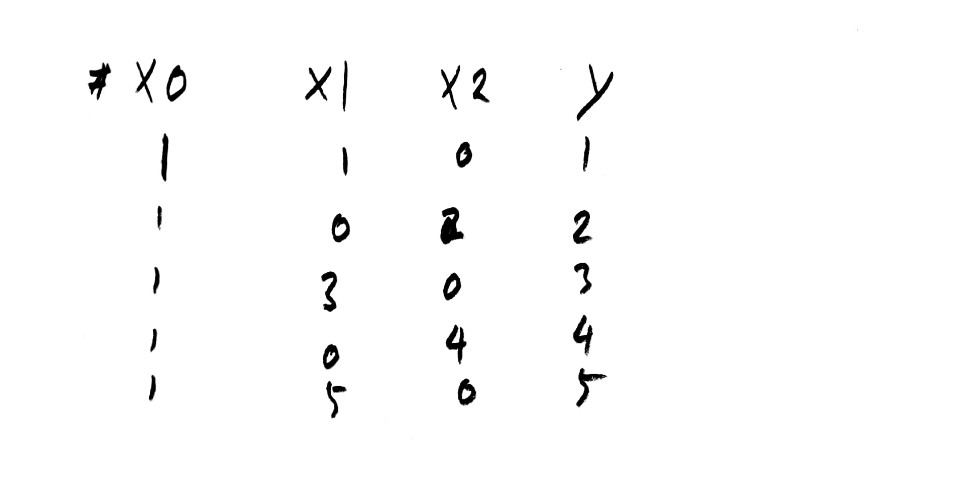One example of where this handcoded approach will fail is in detecting faces in images. Today, every smartphone can detect a face in an image.
The most successful kinds of machine learning algorithms are those that automate decision-making processes by generalizing from known examples
In this setting, which is known as supervised learning
the user provides the algorithm with pairs of inputs and desired outputs, and the algorithm finds a way to produce the desired output given an input.
scikit-learn is a very popular tool, and the most prominent Python library for machine learning.
A Python distribution made for large-scale data processing, predictive analytics, and scientific computing
1 | pip install numpy scipy matplotlib ipython scikit-learn pandas pillow |
1 | scikit-learn` is built on top of the NumPy and SciPy scientific Python libraries. In addition to NumPy and SciPy, we will be using `pandas` and `matplotlib |
1 | import numpy as np |
pandas is a Python library for data wrangling and analysis
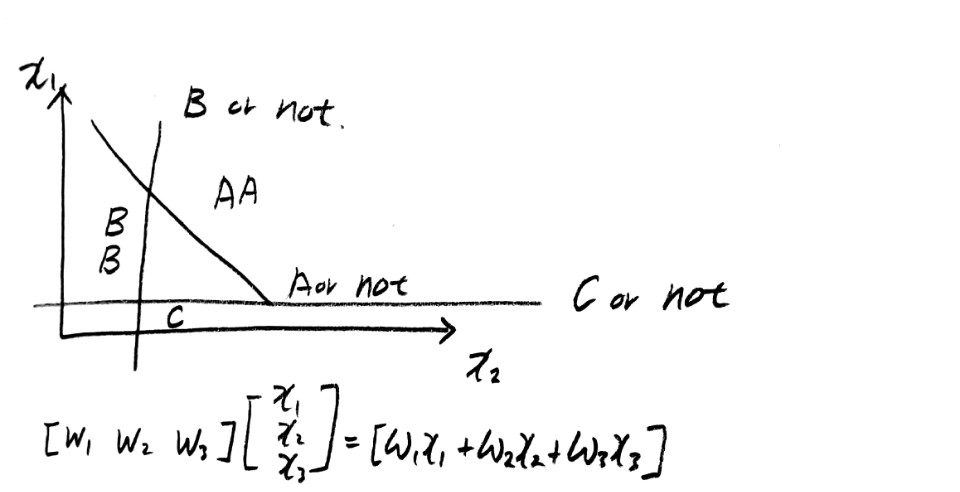
classification
어떤 데이터들을 분류하는 문제이다.
여기서 분류의 대상의 data, 분류종류를 class 그리고 특정 데이터가 분류되었을때 그 분류 이름을 label이라고 부른다.