자료구조 | 정렬(sorting)

개요

컴퓨터 안에는 수십 수만가지의 데이터 들이 있으며, 이러한 수많은 데이터들을 잘 정리하고 보관하는 것은 빠른 데이터 찾기와 데이터 추가 및 삭제 등의 작업의 효율에 매우 큰 영향을 미친다. 때문에 컴퓨터의 많은 자료들을 효율적으로 분류하고 원하는 자료를 찾고 추가 하기 위해서는 ‘정렬’에 대해 알아야 할 필요가 있다.

본 강의에서 리스트 란 하나 이상의 필드로 된 레코드의 집합이라는 의미로 사용하며, 이때 코드를 서로 구별하기 위해 사용되는 필드를 키 라고 한다.

일반적인 자료의 탐색 방법

흔히 리스트를 탐색하는 가장 직관적인 방법은 앞에서 부터 차례대로 비교하면서 자료를 분류하는 것이다.
프로그래밍에서 for 문을 사용하여 리스트의 제일 앞에서 부터 뒤까지 훑어 가면서 equal 문을 통해 데이터를 찾는 작업은 매우 흔한 프로그래밍의 구현이다.

이렇게 어떤 리스트의 왼편에서 오른편으로 차례대로 데이터를 찾는 것을 순차 탐색 이라고 한다.

다음 C 언어로 순차탐색 프로그램을 구현한 코드이다.

#include <iostream>
using namespace std;

struct Element
{
  public:
    string key;
};

int seqSearch(Element elements[], string key)
{
    int i;
    int count = sizeof(*elements) / sizeof(elements[0]);
    cout << "address of the elements: " << elements << endl;
    cout << "count is: " << count << endl;
    for (i = 0; i < count; i++)
    {
        if (elements[i].key == key)
        {
            return i;
        };
    };
    return 0;
};

int main(void)
{
    Element element1 = {"123"};
    Element element2 = {"namhoon"};
    Element elements[] = {element1, element2};
    int result = seqSearch(elements, "namhoon");
    cout << result;
}

위 프로그램을 살펴보면 for 문을 돌면서 n 개의 레코드를 탐색하는 평균은 (n+1)/2 이므로, O(n)의 시간복잡도를 가진다.

만약 어떤 리스트가 정렬된 순차 리스트라면 이런 순차 탐색 말고 이원 탐색 을 사용하여 자료를 찾을 수 있으며 이 경우 시간 복잡도는 O(logn) 이다.

정렬의 종류

삽입 정렬

i 개의 정렬된 레코드에 새로운 레코드를 끼워넣어 i+1 개의 정렬된 레코드 리스트를 만드는 정렬 방법이다.

아래 프로그램은 C로 구현한 insert 함수이다.

정렬된 리스트 a[1:i] 에 e 원소를 집어넣어 a[1:i+1]의 리스트를 만들어 내는 함수이다.

index 역할을 하는 i가 점차 작아지면서 a[i].key가 e.key 보다 큰 경우 한칸씩 우측으로 밀어내고, a[i].key가 e.key 보다 작아지는 i 값에서 a[i+1]에 e를 넣어준다.

void insert(element e, element a[], int i){
  a[0]=e;
  while(e.key<a[i].key){
    a[i+1] = a[i];
    i--;
  }

  a[i+1] = e;
}

아래 함수는 insert 함수를 활용하여 삽입정렬을 하는 프로그램이다.

void insertionSort(element a[], int n){
  int j;
  for(j=2;j<=n;j++){
    element temp = a[j];
    insert(temp, a, j-1);
  }
}

병합정렬(Merge Sort)

병합정렬은 입력 리스트를 길이가 1인 n 개의 정렬될 서브트리로 간주하는 것으로 시작합니다.

아래 merge 함수는 두개의 서로 다른 리스트를 병합하는 것을 보여줍니다.

merge sort 의 각 단계는 O(n) 의 시간이 걸리고 logn 번의 단계가 적용되므로 O(nlogn) 의 복잡도를 가집니다.

Time Complexity: O(nlogn)

또한 각 병합과정에서 새로운 배열이 필요하므로 inplace sort가 아니다.

퀵 정렬(Quick Sort)

퀵 정렬은 앞서 살펴본 정렬법 중에서 가장 좋은 평균 성능을 가지고 있다.
퀵 정렬의 순서는 먼저 피벗 레코드를 선택하여 피벗의 왼쪽에는 레코드 키들이 피벗의 키보다 작거나 같고 피벗의 오른쪽에는 레코드 키들이 피벗의 키보다 크거나 같도록 하는 방법을 사용한다. 최종적으로는 피벗의 왼쪽에 있는 레코드들과 피벗의 오른쪽에 있는 레코드들이 서로 독립적으로 정렬이 된다.

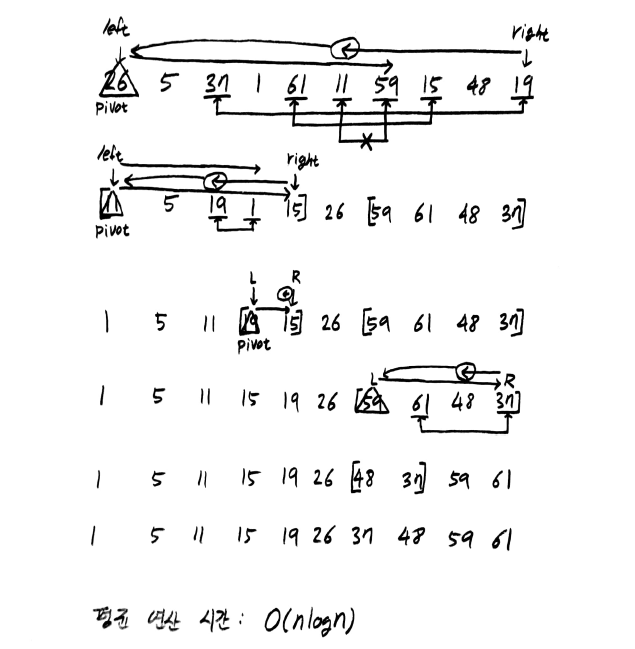
다음은 퀵 정렬을 수행하는 프로그램이다.
i와 j가 각각 왼쪽과 오른쪽에서 가운데 방향으로 진행하며, a[i].key는 pivot 보다 커질 때까지 a[j].key는 pivot 보다 작아질 때 까지

void quickSort(element a[], int left, int right){
  int pivot,i,j;
  pivot = a[left].key;
  do{
    do j++;while(a[i].key<pivot);
    do j--;while(a[j].key>pivot);
  }
}

히프정렬

히프 정렬에서는 최대 길이 [log_2(n+1)] 을 가지고 adjust를 n-1번 호출한다.

즉, O(nlogn) 이다.

버블 정렬

선택 정렬

---